Portfolio optimization and index tracking have been the two key topics in long-term research in both academia and business. In modern finance, financial investors, especially institutional ones, routinely work with a large number of assets. The large dimension of assets brings two great challenges: extensive computation time and large estimation errors. This project employs regularization techniques to accommodate these challenges. The basic idea of regularization techniques is to reduce the number of parameter estimates for improving estimation accuracy by shrinking many close-to-zero estimates towards zero. In particular, this project develops a framework based on the regularization of sample eigenvalues to estimate the inverse covariance matrix of asset return in high dimensional portfolio selection. The proposed framework enables us to derive a closed form solution to the optimal shrinkage density of the sample eigenvalues, which greatly reduces the computation time. In sparse index tracking, this project develops the adaptive elastic net (Aenet) approach and the coordinate-descent algorithm for speeding up the solution procedure. These techniques have been cited and applied in various areas.

Fig 1 Registration of computer software copyright: High-dimensional portfolio optimization based on eigenvalue regularization 1.0

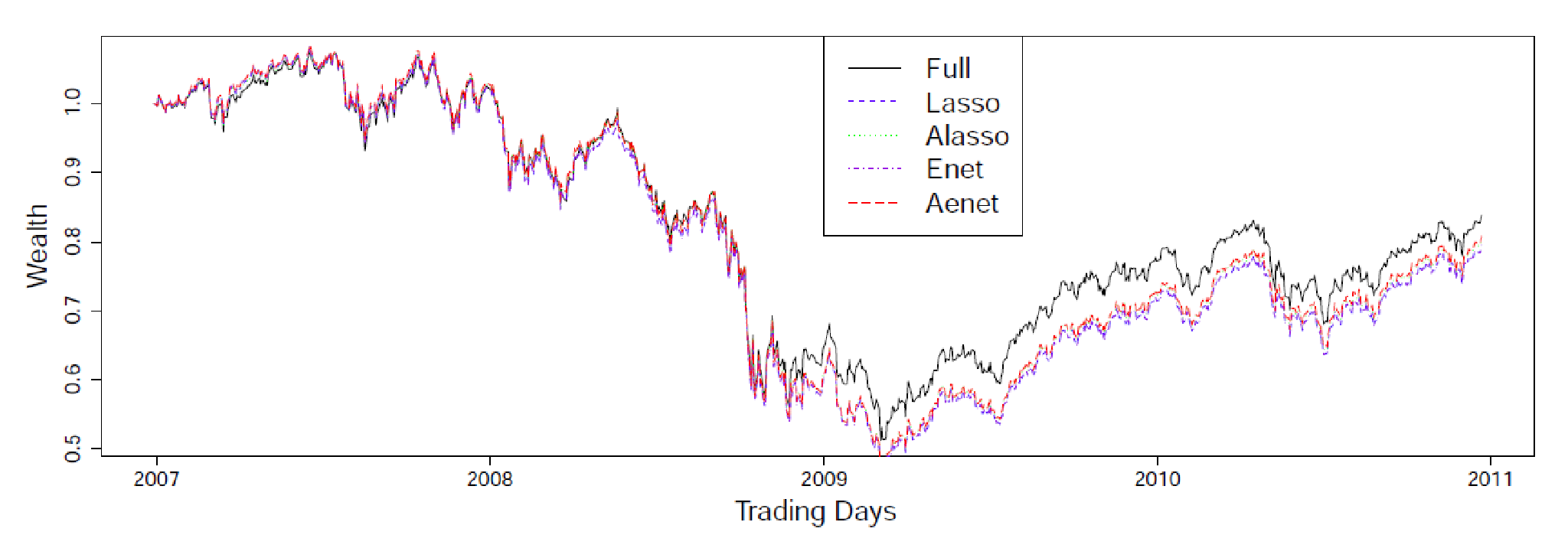
Fig 2 The wealth growth over the trading horizon among sparse index tracking approaches based on Lasso, Alasso, Enet, and Aenet for the data set FTSE100 (Full: full replication or true index return).