This project studies numerical methods for differential equations. Fractional differentiation and integration generalize the classic integer-order ones to arbitrary real-valued order. Differential equations with fractional derivatives have attracted increasing attention due to its practical applications in viscoelastic models and image processing etc. Since exact solutions to differential equations with fractional derivatives are usually not available, numerical methods for solving such equations are of great interest. However, due to the historical dependence of fractional derivatives, it is challenging to extend classical high-order methods to these equations. We developed several discretization formulas which can also be used for linearized schemes to nonlinear differential equations with fractional derivatives. Furthermore, some efficient algorithms were proposed to reduce computational cost of the schemes.

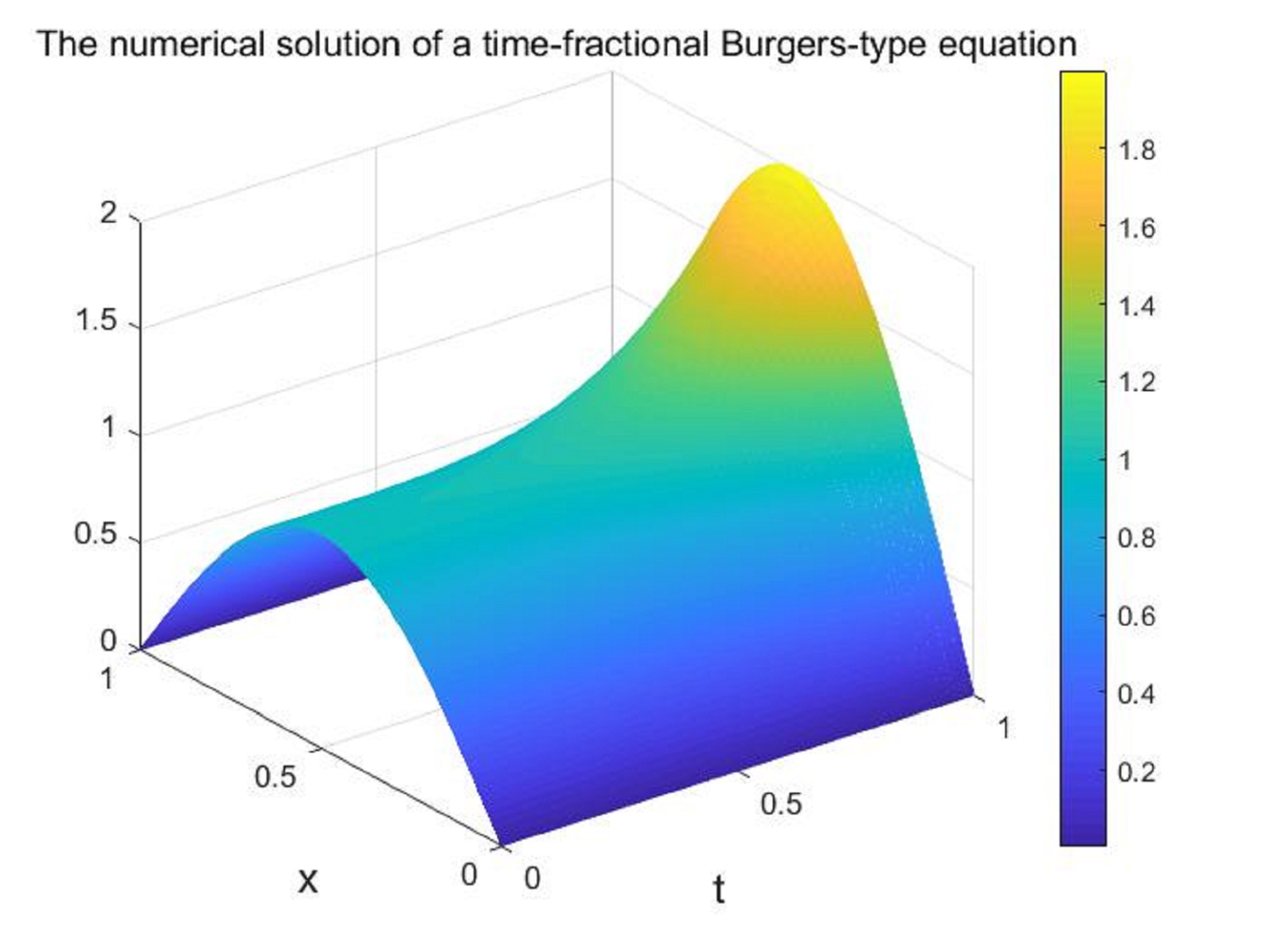
Fig 1 Numerical solution of a time-fractional Burgers-type equation: High-order linearized scheme